OmniSimOmni-directional photonic simulations |
    |
Modelling Gratings with RCWASimulation of infinitely periodic gratings with OmniSim RCWA softwareWe will show you here how to use OmniSim's RCWA engine to model an infinitely periodic diffraction grating illuminated with oblique incidence. Different approaches can be used to model diffraction gratings:
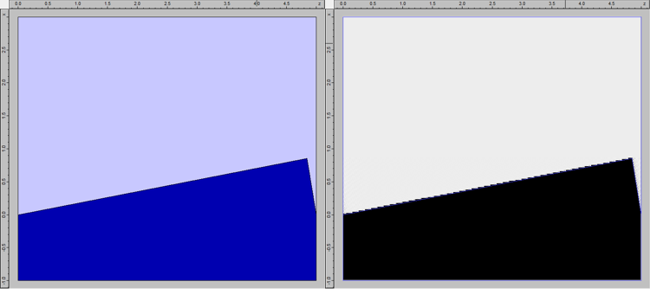
The RCWA approach is ideal as it allows you to calculate how much light is coupled to each diffraction order as well as how much light is absorbed; you would not be able to obtain this information with precision with an FDTD or FETD engine. Designing the unit cell for the infinitely periodic gratingWhen modelling the infinitely periodic grating, we only need to consider a single period of the grating. The design is shown below on the left-hand side. The dark blue region corresponds to the silver grating, and the pale blue region to air. On the right-hand side you can see the structure as it is rendered by the Fourier series of the RCWA engine.
The design settings are given in the table below.
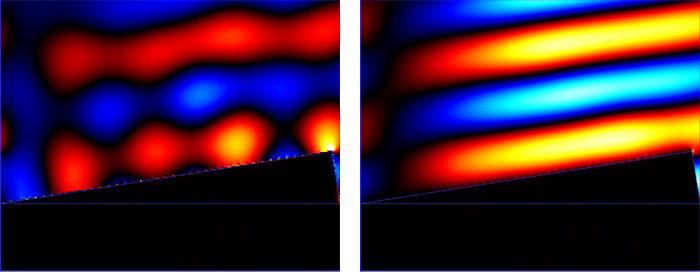
Modelling the diffraction grating with RCWAThe structure is illuminated with a tilted plane wave excitation; the RCWA engine allows you to control the orientation of the illumination by rotating the plane wave both in-plane and out-of-plane. You can see below the Ex component of the nearfield profile resulting from the RCWA simulation.
RCWA is a modal method and it allows us to calculate how much power is coupled to each diffraction order with precision. The results obtained after the RCWA calculation are given in the table below. Most of power is coupled to the diffraction of order m=1, and a small amount is coupled to the other orders of diffraction. The remaining 5.01% of power was absorbed in the metal.
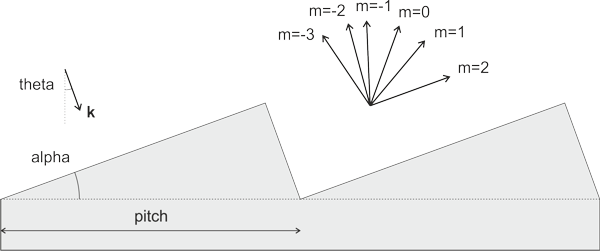
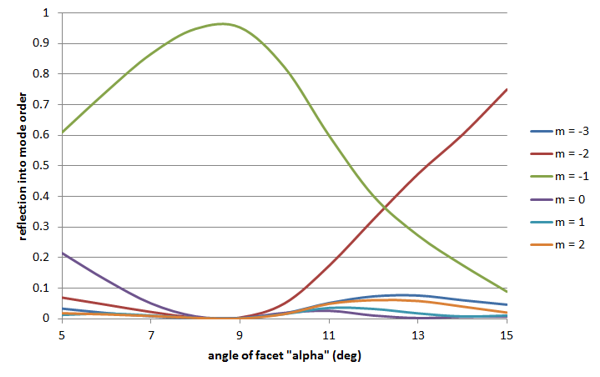
The convergence of the results was studied when varying the number of modes used in the RCWA calculation and the number of layers used to discretise the tilted profile of the grating. The RCWA Engine was able to provide initial results in under 10s and converged results with a high accuracy in 2.9 minutes on a computer with a dual-Xeon E5-2630v3 CPU. Scanning the orientation of the facetsWe used the RCWA scanner to study the variation of the reflected power in each diffraction order when varying the orientation "alpha" of the facet, the orientation "theta" of the illumination being kept constant. The results are shown below. The order m = -1 (closest to the direction of the incident beam) receives maximum power for an angle of 8.7 degrees; as the tilt of the facets increases, an increasing amount of light couples into m = -2 (closer to the grating plane).
Modelling Echelle gratings and WDM devicesIf you are interested in modelling diffraction gratings for use in echelle gratings and WDM Devices, please have a look at Epipprop, our unique echelle grating model.
|